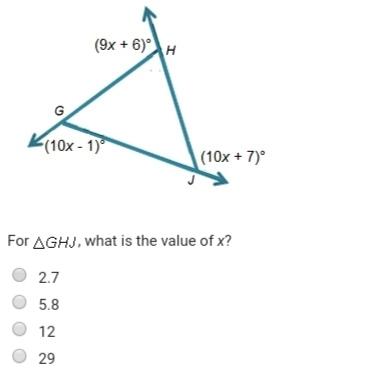
Mathematics, 06.05.2020 04:30 lucindabarba2017
In this activity, you will explore how similarity transformations establish similarity for all circles. Open the GeoGebra geometry tool, and complete each step below.
Part A
Start by creating two different circles:
• Create a point, and label it A. To make the remainder of the activity easier, choose integers for the x and y coordinates of point A.
• Create a circle with its center at point A and with a radius of your choice. To make the remainder of the activity easier, choose an integer value for the radius.
• Create another point, and label it B. To make the remainder of the activity easier, choose integers for the x and y coordinates of the point.
• Create a circle with its center at point B and with a radius of your choice that is different from the radius chosen for circle A. To make the remainder of the activity easier, choose an integer value for the radius.
Take a screenshot of the two circles you created, save it, and insert the image in the space provided.
Part B
Recall what you know about similarity. If circle B is similar to circle A, what must exist?
Part C
What is the difference of the x-coordinate of point A and the x-coordinate of point B?
Part D
In terms of rigid transformations (reflections, rotations, and translations), what does this difference represent?
Part E
What is the difference of the y-coordinate of point A and the y-coordinate of point B?
Part F
In terms of rigid transformations (reflections, rotations, and translations), what does this difference represent?
Part G
What is the ratio of the radius of circle A to the radius of circle B?
Part H
In terms of nonrigid transformations, what does this ratio represent?
Part I
Write a sequence of dilations and translations that maps circle B onto circle A.
Part J
What is the relationship between circle A and circle B?
Part K
You have established that circles A and B are similar. What conclusion can you make about any two given circles?
Part L
For assurance that the similarity proof can be generalized to all circles, try more examples of creating two circles and determining the similarity transformations that map one circle onto the other circle. Take a screenshot of two such circles, labeled C and D, that are different from the ones created in part A, save it, and insert the image in the space provided.
Part M
Write a sequence of dilations and translations that maps circle D onto circle C and that shows the two circles you created are similar.

Answers: 2


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 21:30, stichgotrich849
Janice determined there were 10 possible outcomes when tossing two coins and spinning a spinner numbered 1 through 6. what is the correct number? what might have been janice's error?
Answers: 3

You know the right answer?
In this activity, you will explore how similarity transformations establish similarity for all circl...
Questions in other subjects:


Biology, 18.07.2019 22:30



Medicine, 18.07.2019 22:30



Mathematics, 18.07.2019 22:30