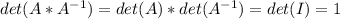Mathematics, 09.04.2020 01:43 justijust500
Show that if A is invertible, then det Upper A Superscript negative 1det A−1equals=StartFraction 1 Over det Upper A EndFraction 1 det A. What theorem(s) should be used to examine the quantity det Upper A Superscript negative 1det A−1? Select all that apply. A. If A and B are ntimes×n matrices, then det ABequals=(det Upper A )(det A)(det Upper B )(det B). Your answer is correct. B. If one row of a square matrix A is multiplied by k to produce B, then det Upper Bdet Bequals=ktimes•(det Upper A )(det A). C. A square matrix A is invertible if and only if det Upper Adet Anot equals≠0. Your answer is correct. D. If A is an ntimes×n matrix, then det Upper A Superscript Upper Tdet ATequals=det Upper Adet A. Consider the quantity (det Upper A )(det Upper A Superscript negative 1 Baseline )(det A)det A−1. To what must this be equal? A. det Upper I

Answers: 3


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:30, WhiteWinterRose
Which equation represents the line that passes through the points and (4, 10) and (2, 7)? y = 3/2x - 11y = 3/2x +4y = - 3/2x + 19y = - 3/2x + 16
Answers: 2

Mathematics, 21.06.2019 17:00, cjd1214812148
The rectangle on the right is the image of the rectangle on the left. what transformation would result in this image? reflection rotation translation dilation
Answers: 2

Mathematics, 21.06.2019 19:50, nawafcanada
On a piece of paper graft y+2> -3x-3 then determine which answer matches the graph you drew
Answers: 2
You know the right answer?
Show that if A is invertible, then det Upper A Superscript negative 1det A−1equals=StartFraction 1 O...
Questions in other subjects:

Mathematics, 20.05.2021 04:30




English, 20.05.2021 04:30

Spanish, 20.05.2021 04:30

Biology, 20.05.2021 04:30

Mathematics, 20.05.2021 04:30

Geography, 20.05.2021 04:30

Mathematics, 20.05.2021 04:30

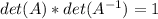 and
and 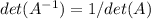
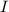 = Identity Matrix
= Identity Matrix 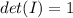 .
. 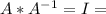 Identity Matrix.
Identity Matrix.