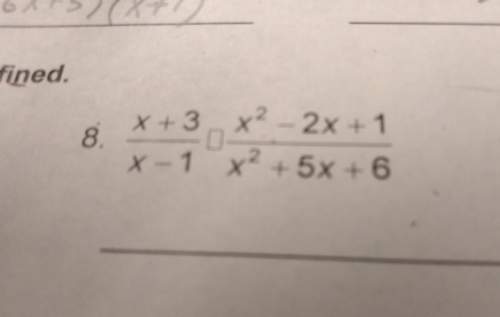Mathematics, 31.08.2019 15:20 PKTHUNDER5011
Given the function f(x) = x2 and k = 3, which of the following represents the graph becoming more narrow?
a. f(x)+k
b. kf(x)
c. f(x+k)
d. f(k-x)

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 14:00, flowergirly34
Demonstrate the proof of your new polynomial identity through an algebraic proof and a numerical proof in an engaging way! make it so the whole world wants to purchase your polynomial identity and can't imagine living without it! you must: label and display your new polynomial identity prove that it is true through an algebraic proof, identifying each step demonstrate that your polynomial identity works on numerical relationships create your own using the columns below. see what happens when different binomials or trinomials are combined. square one factor from column a and add it to one factor from column b to develop your own identity. column a column b (x − y) (x2 + 2xy + y2) (x + y) (x2 − 2xy + y2) (y + x) (ax + b) (y − x) (cy + d)
Answers: 3

Mathematics, 21.06.2019 17:00, Zykuko
Asays "we are both knaves" and b says nothing. exercises 24–31 relate to inhabitants of an island on which there are three kinds of people: knights who always tell the truth, knaves who always lie, and spies (called normals by smullyan [sm78]) who can either lie or tell the truth. you encounter three people, a, b, and c. you know one of these people is a knight, one is a knave, and one is a spy. each of the three people knows the type of person each of other two is. for each of these situations, if possible, determine whether there is a unique solution and determine who the knave, knight, and spy are. when there is no unique solution, list all possible solutions or state that there are no solutions. 24. a says "c is the knave," b says, "a is the knight," and c says "i am the spy."
Answers: 2

Mathematics, 21.06.2019 19:40, evarod
Afactory makes propeller drive shafts for ships. a quality assurance engineer at the factory needs to estimate the true mean length of the shafts. she randomly selects four drive shafts made at the factory, measures their lengths, and finds their sample mean to be 1000 mm. the lengths are known to follow a normal distribution whose standard deviation is 2 mm. calculate a 95% confidence interval for the true mean length of the shafts. input your answers for the margin of error, lower bound, and upper bound.
Answers: 3

Mathematics, 21.06.2019 22:00, Jasten
Set $r$ is a set of rectangles such that (1) only the grid points shown here are used as vertices, (2) all sides are vertical or horizontal and (3) no two rectangles in the set are congruent. if $r$ contains the maximum possible number of rectangles given these conditions, what fraction of the rectangles in set $r$ are squares? express your answer as a common fraction.
Answers: 1
You know the right answer?
Given the function f(x) = x2 and k = 3, which of the following represents the graph becoming more na...
Questions in other subjects:



Health, 17.12.2020 06:00

English, 17.12.2020 06:00

Mathematics, 17.12.2020 06:00

Mathematics, 17.12.2020 06:00


Mathematics, 17.12.2020 06:00

Mathematics, 17.12.2020 06:00

![\left[\begin{array}{ccc}a\\b\end{array}\right]](/tpl/images/0215/2504/0c6ab.png) results in the graph defined by y - b = f(x - a). This is done by replacing x with (x - a) and y with (y - b). Finally it is rearranged to make y the subject, as is often the convention: y = f(x - a) + b.
results in the graph defined by y - b = f(x - a). This is done by replacing x with (x - a) and y with (y - b). Finally it is rearranged to make y the subject, as is often the convention: y = f(x - a) + b.