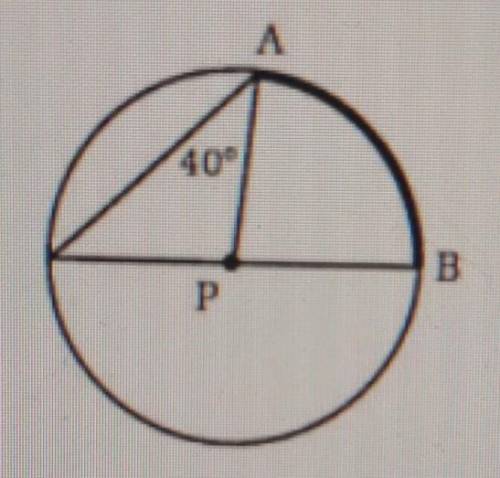
If a point on circle p is selected at random, what is the probability that it lines on Arc AB?
...

Mathematics, 16.07.2021 07:20 sunny3799
If a point on circle p is selected at random, what is the probability that it lines on Arc AB?

Answers: 2


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 16:20, whitneyt3218
7.(03.01 lc)which set represents the range of the function shown? {(-1, 5), (2,8), (5, 3), 13, -4)} (5 points){-1, 2, 5, 13){(5, -1), (8, 2), (3,5), (-4, 13)){-4, 3, 5, 8}{-4, -1, 2, 3, 5, 5, 8, 13}
Answers: 3

Mathematics, 21.06.2019 17:00, samantha9430
The magnitude, m, of an earthquake is defined to be m=log l/s, where i is the intensity of the earthquake (measured by the amplitude of the seismograph wave) and s is the intensity of a “standard” earthquake, which is barely detectable. what is the magnitude of an earthquake that is 1,000 times more intense than a standard earthquake? use a calculator. round your answer to the nearest tenth.
Answers: 1

Mathematics, 21.06.2019 19:30, estherstlouis7812
1. find the area of the unshaded square 2. find the area of the large square 3. what is the area of the frame represented by the shaded region show
Answers: 1

Mathematics, 21.06.2019 20:30, maxy7347go
Does the function satisfy the hypotheses of the mean value theorem on the given interval? f(x) = 4x^2 + 3x + 4, [−1, 1] no, f is continuous on [−1, 1] but not differentiable on (−1, 1). no, f is not continuous on [−1, 1]. yes, f is continuous on [−1, 1] and differentiable on (−1, 1) since polynomials are continuous and differentiable on . there is not enough information to verify if this function satisfies the mean value theorem. yes, it does not matter if f is continuous or differentiable; every function satisfies the mean value theorem.
Answers: 1
You know the right answer?
Questions in other subjects:

Biology, 27.10.2020 18:20


Biology, 27.10.2020 18:20


Chemistry, 27.10.2020 18:20




Mathematics, 27.10.2020 18:20




