Golden Ellipse
Calculus Level 5
Consider an ellipse whose semi-axes have lengths aa and...

Mathematics, 03.06.2021 09:30 ewaltz74
Golden Ellipse
Calculus Level 5
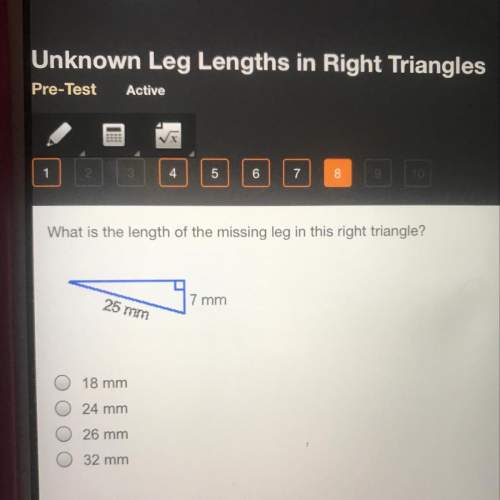
Consider an ellipse whose semi-axes have lengths aa and bb, where {a>b}a>b. A chord in this ellipse makes acute angles \alphaα and \betaβ with the ellipse. Let \beta_{\text{min}}β
min
denote the minimum possible value of \betaβ, for a given value of \alphaα. Evaluate \beta_{\text{min}}β
min
as a function of \alphaα.
Now, take the ratio of the semi-axes of the ellipse to be \varphiφ (the golden ratio), and submit your answer as the value of {\displaystyle\int_{0}^{\frac{\pi}{ 2}}\tan\left(\beta_{\text{min}}\rig ht)\,d\alpha}∫
0
2
π
tan(β
min
)dα.

Answers: 1


Other questions on the subject: Mathematics



Mathematics, 21.06.2019 21:00, taylordalton93
Factor the trinomial below. 12x^2 - 32x - 12 a. 4(3x+3)(x-1) b. 4(3x+1)(x-3) c. 4(3x+6)(x-2) d. 4(3x+2)(x-6)
Answers: 2

Mathematics, 21.06.2019 23:00, tfyvcu5344
The weight of a radioactive isotope was 96 grams at the start of an experiment. after one hour, the weight of the isotope was half of its initial weight. after two hours, the weight of the isotope was half of its weight the previous hour. if this pattern continues, which of the following graphs represents the weight of the radioactive isotope over time? a. graph w b. graph x c. graph y d. graph z
Answers: 2
You know the right answer?
Questions in other subjects:





Mathematics, 29.09.2020 14:01



Mathematics, 29.09.2020 14:01

English, 29.09.2020 14:01