
Mathematics, 23.05.2021 21:20 Kigarya
Let A be a matrix with independent rows. A. Show that AAT is invertible. B. Show that if b is any vector in Col(A), then the equation Ax = b has a solution in Row(A) given by xR = AT (AAT )−1 b. (The matrix AT (AAT )−1 is called the pseudoinverse of A, and is usually denoted by A+ . It is a right inverse of A, and coincides with the two-sided inverse A−1 if A is square.) c. The mapping of Col(A) to Row(A) given by xR = AT (AAT )−1 b is an isomorphism

Answers: 2


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:00, NicoleQuinn
Find the sum of the measure of the interior angles of a polygon of 9 sides ; of 32 sides
Answers: 1

Mathematics, 21.06.2019 15:20, queentynaisa
Which is the equation of an ellipse with directrices at x = ±4 and foci at (2, 0) and (−2, 0)?
Answers: 3

You know the right answer?
Let A be a matrix with independent rows. A. Show that AAT is invertible. B. Show that if b is any ve...
Questions in other subjects:

Biology, 01.08.2019 20:00

Social Studies, 01.08.2019 20:00

Biology, 01.08.2019 20:00





Mathematics, 01.08.2019 20:00


Biology, 01.08.2019 20:00

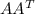 is invertible
is invertible 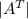 ≠ 0
≠ 0 = | A |
= | A | 


