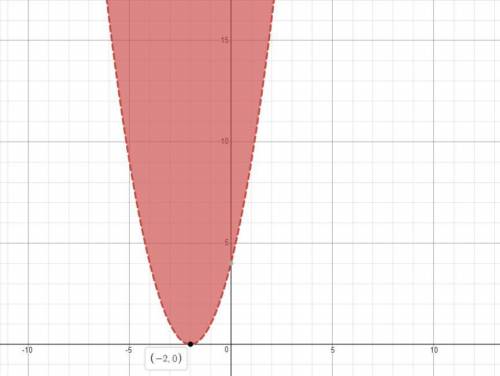
Click on all that are true about the graph of y > x^2 + 4x + 4.

a. the parabola opens up.
b. the line of symmetry is y = -2.
c. the vertex is at (-2, 0).
d. the parabola is dashed.
e. the parabola is shaded outside.

Suppose we have a set of small wooden blocks showing the 26 letters of the english alphabet, one letter per block. (think of scrabble tiles.) our set includes 10 copies of each letter. we place them into a bag and draw out one block at a time. (a) if we line up the letters on a rack as we draw them, how different ways coukl we fill a rack of 5 letters? (b) now suppose we just toss our chosen blocks into a pile, and whenever we draw a letter we already have, we put it back in the bag and draw again. how many different piles of 5 blocks could result? possible? piles will contain at least one repeated letter? (c) if we draw out 5 blocks wit hout looking at them, how many different piles are (d) if we draw out 5 blocks without looking at them, how many of the possible 2. (4) consider the following formula. 12 give two different proofs, one using the factorial formulas and the other combina torial.