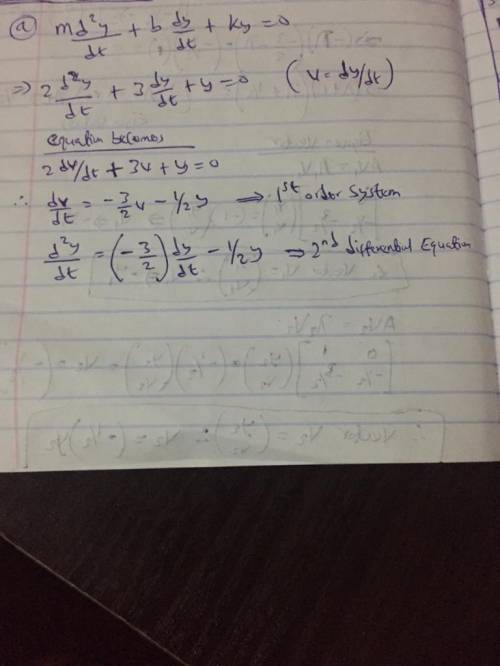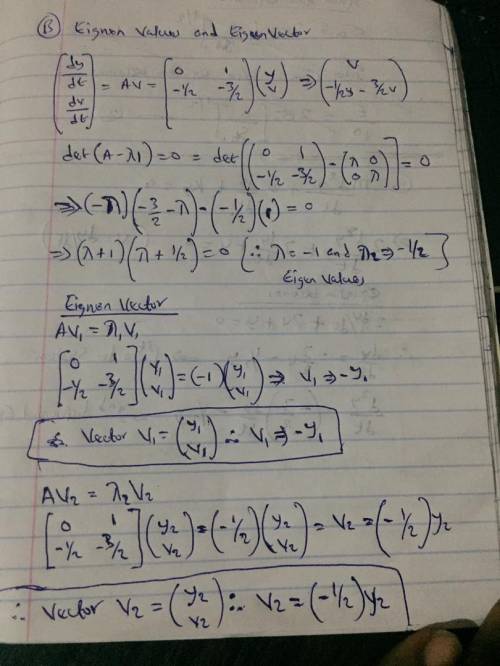Mathematics, 16.04.2021 18:40 qloc
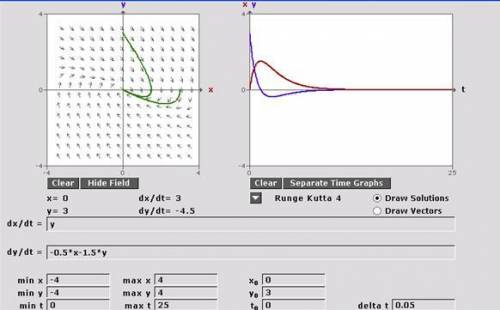
Consider harmonic oscillators with mass m, spring constant k, and damping coefficient b. For the values specified,
a. write the second-order differential equation and the corresponding first-order system.
b. find the eigenvalues and eigenvectors of the linear system.
c. classify the oscillator (as underdamped, overdamped, critically damped, or undamped) and, when appropriate, give the natural period.
d. sketch the phase portrait of the associated linear system and include the solution curve for the given initial condition.

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 17:00, KendallTishie724
In the given figure ar(adf) =ar(cda) and ar(cdf) = ar(cdf). show that abdc and cdfe are trapeziums.
Answers: 2

Mathematics, 21.06.2019 20:30, ciannajustine
Drag the tiles to the correct boxes to complete the pairs. not all tiles will be used. match each division expression with the correct quotient.
Answers: 2

Mathematics, 21.06.2019 23:00, jetblackcap
Perry observes the opposite parallel walls of a room in how many lines do the plains containing the walls intersect
Answers: 1

You know the right answer?
Consider harmonic oscillators with mass m, spring constant k, and damping coefficient b. For the val...
Questions in other subjects:

Chemistry, 29.04.2021 08:20


Chemistry, 29.04.2021 08:20


Mathematics, 29.04.2021 08:20

Mathematics, 29.04.2021 08:20




Mathematics, 29.04.2021 08:20