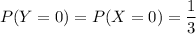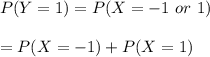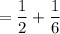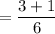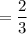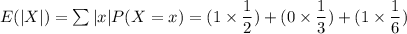Mathematics, 02.02.2021 03:50 stormserena

Let X have the probability mass function P(X = −1) = 1 2 , P(X = 0) = 1 3 , P(X = 1) = 1 6 Calculate E(|X|) using the approaches in (a) and (b) below. (a) First find the probability mass function of the random variable Y = |X| and using that compute E(|X|). (b) Apply formula (3.24) with g(x) = |x|. For reference, formula 3.24 states

Answers: 1

Show answers

Other questions on the subject: Mathematics

Mathematics, 22.06.2019 02:30, ImmortalEnigmaYT

Translate the algebraic expression shown below into a verbal expression. fraction with variable x in numerator and 6 in the denominator. the sum of six and some number the product of six and some number the quotient of some number and six the difference of six and some number

Answers: 1

continue

Mathematics, 22.06.2019 03:00, ava5015

What is the missing value in the proportion 4/5 = x/30

Answers: 2

continue

Mathematics, 22.06.2019 04:10, wmaingrette1

3.(03.01)the domain of the following relation r {(6, -2), (1, 2), (-3, -4), (-3, 2)} is (1 point)o {-4, -2, 2)^{-3, -3, 1,6}{-4, -2, 2, 2){-3, 1, 6)4.(03.01)dulan created color nanele for a wall usinn a mix of only arepn and blue naints haplotted the quantidescription+

Answers: 3

continue

Mathematics, 22.06.2019 04:20, rclara34oxbrr9

Yes8. (03.01)the range of a relation is (1 point)a set of points that pair input values with output valuesx and y values written in the form (x, y)the output (y) values of the relationthe input (x) values of the relation0description

Answers: 3

continue

You know the right answer?

Let X have the probability mass function P(X = −1) = 1 2 , P(X = 0) = 1 3 , P(X = 1) = 1 6 Calculate...