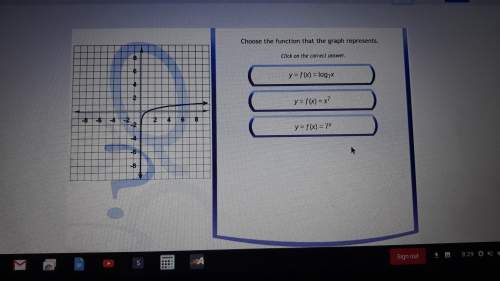
Mathematics, 17.12.2020 22:40 lexieforlife911
PLEASE HELLP
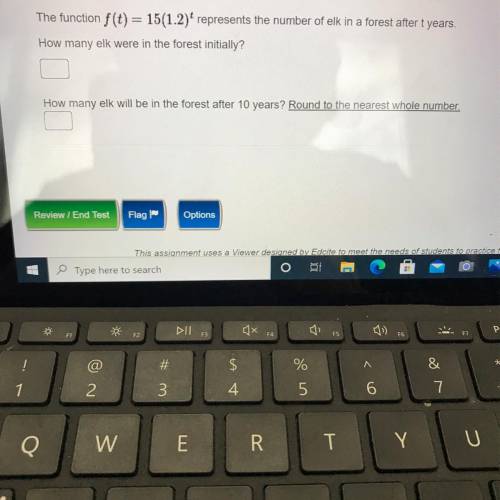

Answers: 1


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 20:30, cheating53
Kayaks rent for $35 per day. which expression can you use to find the cost in dollars of renting 3 kayaks for a day?
Answers: 1

Mathematics, 21.06.2019 21:30, chrisgramjooooo2366
In δabc shown below, ∠bac is congruent to ∠bca: triangle abc, where angles a and c are congruent given: base ∠bac and ∠acb are congruent. prove: δabc is an isosceles triangle. when completed (fill in the blanks), the following paragraph proves that line segment ab is congruent to line segment bc making δabc an isosceles triangle. (4 points) construct a perpendicular bisector from point b to line segment ac . label the point of intersection between this perpendicular bisector and line segment ac as point d: m∠bda and m∠bdc is 90° by the definition of a perpendicular bisector. ∠bda is congruent to ∠bdc by the definition of congruent angles. line segment ad is congruent to line segment dc by by the definition of a perpendicular bisector. δbad is congruent to δbcd by the line segment ab is congruent to line segment bc because consequently, δabc is isosceles by definition of an isosceles triangle. 1. corresponding parts of congruent triangles are congruent (cpctc) 2. the definition of a perpendicular bisector 1. the definition of a perpendicular bisector 2. the definition of congruent angles 1. the definition of congruent angles 2. the definition of a perpendicular bisector 1. angle-side-angle (asa) postulate 2. corresponding parts of congruent triangles are congruent (cpctc)
Answers: 1
You know the right answer?
PLEASE HELLP
...
...
Questions in other subjects:

Mathematics, 01.12.2020 20:30

Mathematics, 01.12.2020 20:30



Business, 01.12.2020 20:30


Mathematics, 01.12.2020 20:30

Mathematics, 01.12.2020 20:30