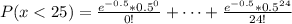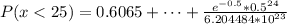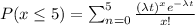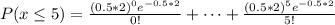Mathematics, 21.10.2020 16:01 ceejay8005
Suppose that minor errors occur on a computer in a space station, which will require re-calculation. Assume the occurrence of errors follows a Poisson process with a rate of 1/2 per hour. (a) Find the probability that no errors occur during a day. (b) Suppose that the system cannot correct more than 25 minor errors in a day, in which case a critical error will arise. What is the probability that a critical error occurs since the start of a day? Keep up to the 6th decimal place in your answer. (c) Suppose the error correction protocols reset themselves so long as there are no more than five minor errors occurring within a 2 hour window. The system just started up and an error occurred. What is the probability the next reset will occur within 2 hours?

Answers: 1


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 18:50, adriana145
The trigonometric ratios sine and secant are reciprocals of each other
Answers: 2


Mathematics, 21.06.2019 20:30, extasisjorge
Ming says that 0.24 > 1/4 because 0.24= 2/4. which best explains mings error
Answers: 1
You know the right answer?
Suppose that minor errors occur on a computer in a space station, which will require re-calculation....
Questions in other subjects:

Mathematics, 11.10.2020 14:01

Mathematics, 11.10.2020 14:01

Physics, 11.10.2020 14:01



English, 11.10.2020 14:01

Mathematics, 11.10.2020 14:01

Mathematics, 11.10.2020 14:01

English, 11.10.2020 14:01

History, 11.10.2020 14:01


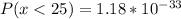
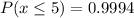
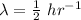 = 0.5 / hr
= 0.5 / hr 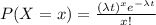
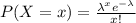
![[tex]P(X = 0) = \frac{\frac{1}{2} ^0 e^{-\frac{1}{2}}}{0!}](/tpl/images/0827/7697/1700c.png)