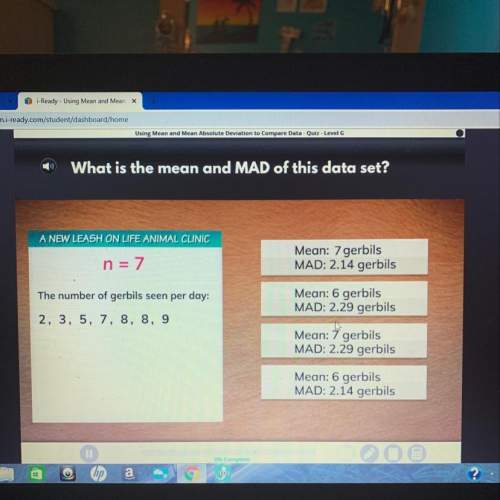
Mathematics, 15.10.2020 08:01 kaylaamberd
A person tosses a fair coin until a tail appears for the first time. If the tail appears on the nth flip, the person wins
2n
dollars. Let X denote the player’s winnings. Show that
E[X]=+[infinity]
This problem is known as the St. Petersburg paradox.
(a) Would you be willing to pay $1 million to play this game once?
(b) Would you be willing to pay $1 million for each game if you could play for as long as you liked and only had to settle up when you stopped playing?

Answers: 3


Other questions on the subject: Mathematics



Mathematics, 21.06.2019 21:30, lilbit217
The map shows the location of the airport and a warehouse in a city. though not displayed on the map, there is also a factory 112 miles due north of the warehouse. a truck traveled from the warehouse to the airport and then to the factory. what is the total number of miles the truck traveled?
Answers: 3

Mathematics, 22.06.2019 01:00, tansebas1107
The table shown below gives the approximate enrollment at the university of michigan every fifty years. how many more students were enrolled at the university of michigan in 1950 than in 1900?
Answers: 3
You know the right answer?
A person tosses a fair coin until a tail appears for the first time. If the tail appears on the nth...
Questions in other subjects:



Mathematics, 25.05.2021 18:10

Mathematics, 25.05.2021 18:10

Geography, 25.05.2021 18:10

Business, 25.05.2021 18:10