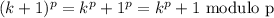Mathematics, 27.08.2020 22:01 kaylastronaut
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which we prove by another method in the next chapter. a) For any integer k with 0 ≤ k ≤ p, let (p k) = p!/k!(p - k)! denote the binomial coefficient. Prove that (p k) 0 mod p if 1 ≤ k ≤ p - 1. b) Prove that for all integers x, y, (x + y)^p x^? + y^p mod p. c) Prove that for all integers x, x^p x mod p.

Answers: 2


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 19:00, sammizwang
Marina baked cookies. she gave 3/4 of the cookies to the scout bake sale. she shared the remaining 6 cookies with her friends. how many cookies did marina bake?
Answers: 3

Mathematics, 21.06.2019 19:00, ktenz
Asmall business produces and sells balls. the fixed costs are $20 and each ball costs $4.32 to produce. each ball sells for $8.32. write the equations for the total cost, c, and the revenue, r, then use the graphing method to determine how many balls must be sold to break even.
Answers: 3
You know the right answer?
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which w...
Questions in other subjects:

Mathematics, 12.12.2021 01:00


Biology, 12.12.2021 01:00



French, 12.12.2021 01:00

Mathematics, 12.12.2021 01:00

Mathematics, 12.12.2021 01:00