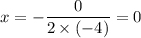Mathematics, 17.08.2020 01:01 bellarae502
Algebraically determine each of the following for the function y=16 - 4x(squared). A) the x and y intercepts if any. B) the symmetry type (x axis, y axis, origin, or neither.)

Answers: 2


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 23:00, Hakika
In january 2010, you began a one-year study of tuberculosis (tb) in a subsidized housing community in the lower east side of new york city. you enrolled 500 residents in your study and checked on their tb status on a monthly basis. at the start of your study on january 1st, you screened all 500 residents. upon screening, you found that 30 of the healthy residents had been vaccinated for tb and therefore were not at risk. another 20 residents already had existing cases of tb on january 1st. on february 1st, 5 residents developed tb. on april 1st, 10 more residents developed tb. on june 1st, 10 healthy residents moved away from new york city and were lost to follow-up. on july 1st, 10 of the residents who had existing tb on january 1st died from their disease. the study ended on december 31, 2010. assume that once a person gets tb, they have it for the duration of the study, and assume that all remaining residents stayed healthy and were not lost to follow-up. is the subsidized housing community in the lower east side of new york city a dynamic or fixed population? briefly explain the rationale for your answer. dynamic population it can changeable people can move out and move in into the population of a subsidized housing what was the prevalence of tb in the screened community on january 1st? prevalence = 30/500 0.06= 6% what was the prevalence of tb on june 30th? prevalence= 40/450=0.08= 8.88% what was the cumulative incidence of tb over the year? cumulative incidence = number of new cases/number in candidate population)over specified time period 10/450 = 2.2% suppose that you wanted to calculate the incidence rate of tb in the study population. calculate the amount of person-time that would go in the denominator of this incidence rate. be sure to show your work.
Answers: 2

Mathematics, 21.06.2019 23:00, naomiedgrey
Look at the chart showing the results of a baseball player at bat. which is the probability of getting a hit?
Answers: 1

Mathematics, 22.06.2019 02:00, Kemosdasavage
What is solution for the following system of equations, 2x+8y=4 and x=-3y+5 1) x=14 y=-3 2) x=2 y=-3 3) x=-3 y=-3 4)x=12 y=5
Answers: 1
You know the right answer?
Algebraically determine each of the following for the function y=16 - 4x(squared). A) the x and y in...
Questions in other subjects:

Biology, 09.06.2020 23:57

Mathematics, 09.06.2020 23:57

Mathematics, 09.06.2020 23:57


Chemistry, 09.06.2020 23:57


Mathematics, 09.06.2020 23:57



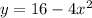
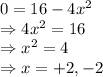
 ,
,