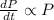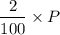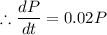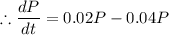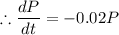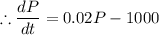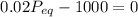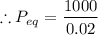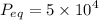Mathematics, 29.07.2020 01:01 titalili0204
Determine a differential equation that models the growth of a population of fish as a function of time in days under each of the following hypotheses:
a) The rate of population increase is proportional to the size of the population. The population increases by 2 percent per day. (Treat time in days as a continuous variable, i. e. the rate at which the population increases is .02 times the population size.) dP/dt =
b) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 4 percent of the population is harvested each day. dP/dt =
c) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 1000 fish are harvested each day. dP/dt =
d) The equation in part c) has a threshhold. What is it?

Answers: 3


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:00, NicoleQuinn
Find the sum of the measure of the interior angles of a polygon of 9 sides ; of 32 sides
Answers: 1

Mathematics, 21.06.2019 20:00, carltonwashington23
The midpoints of the sides of the large square are joined to form a smaller square. what is the area of the smaller square
Answers: 1

Mathematics, 21.06.2019 21:50, spookymod8967
What is the 17th term in the arithmetic sequence in which a6 is 101 and a9 is 83
Answers: 3

Mathematics, 21.06.2019 22:00, alondrachon
Asales representative from a local radio station is trying to convince the owner of a small fitness club to advertise on her station. the representative says that if the owner begins advertising on the station today, the club's total number of members will grow exponentially each month. she uses the given expression to model the number of club members, in hundreds, after advertising for t months.
Answers: 2
You know the right answer?
Determine a differential equation that models the growth of a population of fish as a function of ti...
Questions in other subjects:




Biology, 03.01.2020 01:31


Mathematics, 03.01.2020 01:31

Mathematics, 03.01.2020 01:31