
Mathematics, 29.06.2020 22:01 izabellabyan
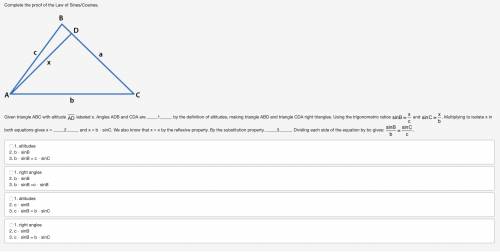
Complete the proof of the Law of Sines/Cosines. Triangle ABC with side b between points A and C, side c between points A and B. Segment drawn from point A to point D where D is between points B and C, segment AD is labeled x. Given triangle ABC with altitude segment AD labeled x. Angles ADB and CDA are _1._ by the definition of altitudes, making triangle ABD and triangle CDA right triangles. Using the trigonometric ratios sine of B equals x over c and sine of C equals x over b. Multiplying to isolate x in both equations gives x = _2._ and x = b ⋅ sinC. We also know that x = x by the reflexive property. By the substitution property, _3._. Dividing each side of the equation by bc gives: sine of B over b equals sine of C over c. 1. altitudes 2. b ⋅ sinB 3. b ⋅ sinB = c ⋅ sinC 1. right angles 2. b ⋅ sinB 3. b ⋅ sinB =c ⋅ sinB 1. altitudes 2. c ⋅ sinB 3. c ⋅ sinB = b ⋅ sinC 1. right angles 2. c ⋅ sinB 3. c ⋅ sinB = b ⋅ sinC

Answers: 1


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 17:10, sanchez626
Determine whether the points (–3,–6) and (2,–8) are in the solution set of the system of inequalities below. x ? –3 y < 5? 3x + 2 a. the point (–3,–6) is not in the solution set, and the point (2,–8) is in the solution set. b. neither of the points is in the solution set. c. the point (–3,–6) is in the solution set, and the point (2,–8) is not in the solution set. d. both points are in the solution set.
Answers: 3

Mathematics, 21.06.2019 21:30, magicpuppydance
On #16 : explain how factoring a trinomial, ax^2+ bx+ c, when a does not equal 1 different from factoring a trinomial when a = 1.
Answers: 2

Mathematics, 21.06.2019 22:00, Jasten
Set $r$ is a set of rectangles such that (1) only the grid points shown here are used as vertices, (2) all sides are vertical or horizontal and (3) no two rectangles in the set are congruent. if $r$ contains the maximum possible number of rectangles given these conditions, what fraction of the rectangles in set $r$ are squares? express your answer as a common fraction.
Answers: 1
You know the right answer?
Complete the proof of the Law of Sines/Cosines. Triangle ABC with side b between points A and C, sid...
Questions in other subjects:


Mathematics, 21.10.2020 01:01







Mathematics, 21.10.2020 01:01

Computers and Technology, 21.10.2020 01:01



