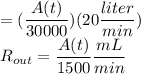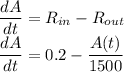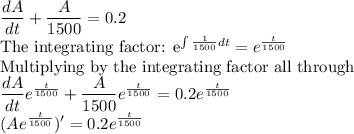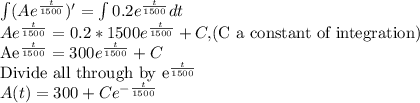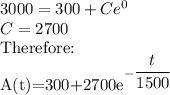A swimming pool with a volume of 30,000 liters originally contains water that is 0.01% chlorine (i. e. it contains 0.1 mL of chlorine per liter). Starting at t = 0, city water containing 0.001% chlorine (0.01 mL of chlorine per liter) is pumped into the pool at a rate of 20 liters/min. The pool water flows out at the same rate. Let A(t) represent the amount of chlorine (in mL) in the tank after t minutes. Write a differential equation for the rate at which the amount of chlorine in the pool is changing with respect to time. Then solve the DE to state a model representing the amount of chlorine in the pool at time t. Be sure to remember to state the initial conditions for this DE clearly.
Rin =
Concentration of chlorine in the tank: c(t) =
Rout =
Differential equation:

Step-by-step explanation:

The volume of the swimming pool = 30,000 liters

(a) Amount of chlorine initially in the tank.

It originally contains water that is 0.01% chlorine.

0.01% of 30000=3000 mL of chlorine per liter

A(0)= 3000 mL of chlorine per liter

(b) Rate at which the chlorine is entering the pool.

City water containing 0.001%(0.01 mL of chlorine per liter) chlorine is pumped into the pool at a rate of 20 liters/min.

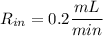
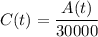
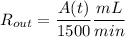
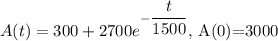
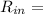(concentration of chlorine in inflow)(input rate of the water)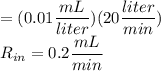

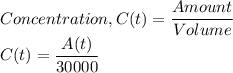
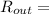(c) Concentration of chlorine in the pool at time t

Volume of the pool =30,000 Liter

(d) Rate at which the chlorine is leaving the pool

(concentration of chlorine in outflow)(output rate of the water)

(e) Differential equation representing the rate at which the amount of sugar in the tank is changing at time t.

We then solve the resulting differential equation by separation of variables.

Taking the integral of both sides

Recall that when t=0, A(t)=3000 (our initial condition)

32

step-by-step explanation: