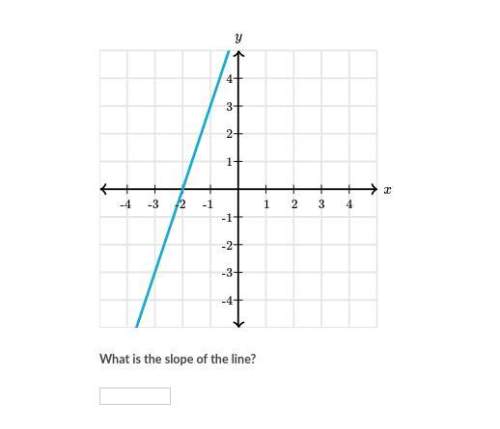
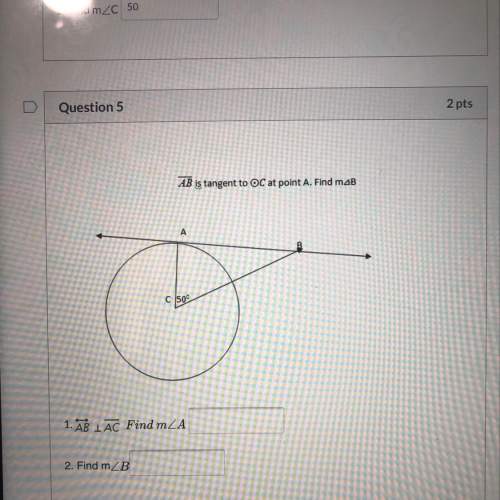
Mathematics, 13.06.2020 01:57 Laners0219
Given $m\geq 2$, denote by $b^{-1}$ the inverse of $b\pmod{m}$. That is, $b^{-1}$ is the residue for which $bb^{-1}\equiv 1\pmod{m}$. Sadie wonders if $(a+b)^{-1}$ is always congruent to $a^{-1}+b^{-1}$ (modulo $m$). She tries the example $a=2$, $b=3$, and $m=7$. Let $L$ be the residue of $(2+3)^{-1}\pmod{7}$, and let $R$ be the residue of $2^{-1}+3^{-1}\pmod{7}$, where $L$ and $R$ are integers from $0$ to $6$ (inclusive). Find $L-R$.

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 20:00, hayleylaw2018
Which fraction is equal to 1hole and 2/5? a.3/5 b.75 c.57 d.73
Answers: 2

Mathematics, 21.06.2019 21:00, ballbritez
Which line is parallel to the line that passes through the points (2, –5) and (–4, 1) a. y=-x+5 b. y=-2/3x+3 c. y=2/3x-2 d. y=x+5
Answers: 2


Mathematics, 22.06.2019 02:00, noobieplayerxd
How many square inches are in 60 square feet?
Answers: 1
You know the right answer?
Given $m\geq 2$, denote by $b^{-1}$ the inverse of $b\pmod{m}$. That is, $b^{-1}$ is the residue for...
Questions in other subjects:

English, 11.12.2019 00:31

Biology, 11.12.2019 00:31



History, 11.12.2019 00:31

History, 11.12.2019 00:31



Biology, 11.12.2019 00:31