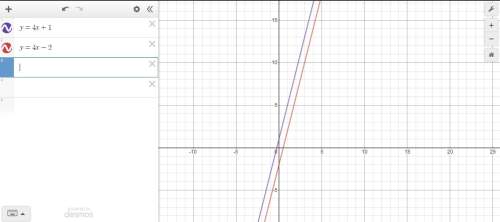
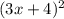Hi can anybody tell me the answer
...

Mathematics, 03.05.2020 14:28 ajflkasjflkasj1168
Hi can anybody tell me the answer
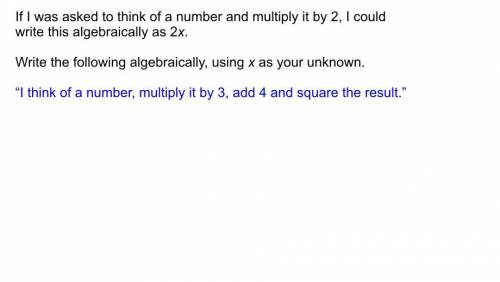

Answers: 3


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:00, jtingley0502
1. are the triangles similar and if so why? what is the value of x? show your work.
Answers: 2

Mathematics, 21.06.2019 21:30, chrisgramjooooo2366
In δabc shown below, ∠bac is congruent to ∠bca: triangle abc, where angles a and c are congruent given: base ∠bac and ∠acb are congruent. prove: δabc is an isosceles triangle. when completed (fill in the blanks), the following paragraph proves that line segment ab is congruent to line segment bc making δabc an isosceles triangle. (4 points) construct a perpendicular bisector from point b to line segment ac . label the point of intersection between this perpendicular bisector and line segment ac as point d: m∠bda and m∠bdc is 90° by the definition of a perpendicular bisector. ∠bda is congruent to ∠bdc by the definition of congruent angles. line segment ad is congruent to line segment dc by by the definition of a perpendicular bisector. δbad is congruent to δbcd by the line segment ab is congruent to line segment bc because consequently, δabc is isosceles by definition of an isosceles triangle. 1. corresponding parts of congruent triangles are congruent (cpctc) 2. the definition of a perpendicular bisector 1. the definition of a perpendicular bisector 2. the definition of congruent angles 1. the definition of congruent angles 2. the definition of a perpendicular bisector 1. angle-side-angle (asa) postulate 2. corresponding parts of congruent triangles are congruent (cpctc)
Answers: 1

Mathematics, 22.06.2019 00:30, gthif13211
I've been working on this for a few days and i just don't understand, it's due in a few hours. you. the direction of a vector is defined as the angle of the vector in relation to a horizontal line. as a standard, this angle is measured counterclockwise from the positive x-axis. the direction or angle of v in the diagram is α. part a: how can you use trigonometric ratios to calculate the direction α of a general vector v = < x, y> similar to the diagram? part b suppose that vector v lies in quadrant ii, quadrant iii, or quadrant iv. how can you use trigonometric ratios to calculate the direction (i. e., angle) of the vector in each of these quadrants with respect to the positive x-axis? the angle between the vector and the positive x-axis will be greater than 90 degrees in each case. part c now try a numerical problem. what is the direction of the vector w = < -1, 6 > ?
Answers: 1
You know the right answer?
Questions in other subjects:



Chemistry, 13.02.2020 18:35