Mathematics, 24.04.2020 18:53 yurimontoya759
The depth of a river at a certain point is modeled by the function W defined above, where W(t) is measured in feet and time t is measured in hours.
(A) Find W′(8) . Using correct units, explain the meaning of W′(8) in the context of the problem.
(B)The graph of W is concave down for 3≤t≤3.5 . Use the line tangent to the graph of W at t=3 to show that W(3.5)≤9
(C) in picture.
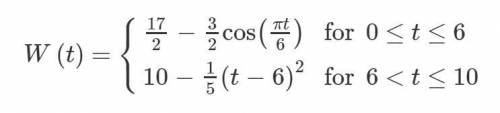
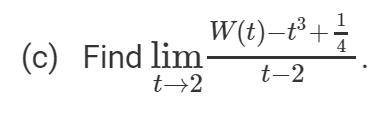

Answers: 2


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 21:30, mandyangle01
Using pert, adam munson was able to determine that the expected project completion time for the construction of a pleasure yacht is 21 months, and the project variance is 4. a) what is the probability that the project will be completed in 17 months? b) what is the probability that the project will be completed in 20 months? c) what is the probability that the project will be completed in 23 months? d) what is the probability that the project will be completed in 25 months? e) what is the due date that yields a 95% chance of completion?
Answers: 3

Mathematics, 21.06.2019 21:40, EvoBruh3273
Drag the tiles to the correct boxes to complete the pairs. using the properties of integer exponents, match each expression with the correct equivalent expression.
Answers: 1

Mathematics, 22.06.2019 04:20, Ahhskii
The weibull distribution is widely used in statistical problems relating to aging of solid insulating materials subjected to aging and stress. use this distribution as a model for time (in hours) to failure of solid insulating specimens subjected to ac voltage. the values of the parameters depend on the voltage and temperature; suppose α = 2.5 and β = 190. (a) what is the probability that a specimen's lifetime is at most 250? less than 250? more than 300? (round your answers to four decimal places.) at most 250 less than 250 more than 300 (b) what is the probability that a specimen's lifetime is between 100 and 250? (round your answer to four decimal places.) (c) what value is such that exactly 50% of all specimens have lifetimes exceeding that value? (round your answer to three decimal places.) hr
Answers: 2
You know the right answer?
The depth of a river at a certain point is modeled by the function W defined above, where W(t) is me...
Questions in other subjects:

Mathematics, 16.04.2020 01:54