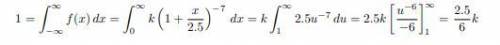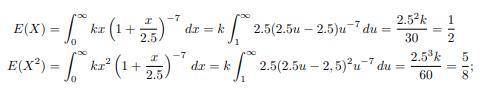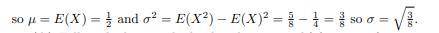Mathematics, 06.04.2020 19:58 ashvinmsingh
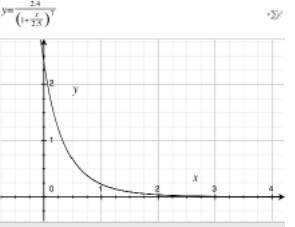
Let X be the total medical expenses (in 1000s of dollars) incurred by a particular individual during a given year. Although X is a discrete random variable, suppose its distribution is quite well approximated by a continuous distribution with pdf f(x) = k 1 + x 2.5 −7 for x ≥ 0.a. What is the value of k?b. Graph the pdf of X. c. What are the expected value and standard deviation of total medical expenses?d. This individual is covered by an insurance plan that entails a $500 deductible provision (so the first $500 worth of expenses are paid by the individual). Then the plan will pay 80% of any additional expenses exceeding $500, and the maximum payment by the individual (including the deductible amount) is $2500. Let Y denote the amount of this individual’s medical expenses paid by the insurance company. What is the expected value of Y? [Hint: First figure out what value of corresponds to the maximum out-of-pocket expense of $2500. Then write an expression for as a function of (which involves several different pieces) and calculate the expected value of this function.]

Answers: 1


Other questions on the subject: Mathematics



Mathematics, 21.06.2019 22:40, zafarm2oxgpmx
Identify this conic section. x2 - y2 = 16 o line circle ellipse parabola hyperbola
Answers: 2

Mathematics, 21.06.2019 23:00, jholland03
Given the expression (7 ? 4i) ? (2 + 6i), perform the indicated operation and write the answer in the form a + bi.
Answers: 1
You know the right answer?
Let X be the total medical expenses (in 1000s of dollars) incurred by a particular individual during...
Questions in other subjects:

Mathematics, 19.01.2021 21:10



Chemistry, 19.01.2021 21:10


Mathematics, 19.01.2021 21:10


Mathematics, 19.01.2021 21:10

Mathematics, 19.01.2021 21:10

Biology, 19.01.2021 21:10