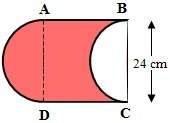
EXAMPLE 4 Find the moments of inertia Ix, Iy, and I0 of a homogeneous disk D with density rho(x, y) = rho, center the origin, and radius a. SOLUTION The boundary of D is the circle x2 + y2 = a2 and in polar coordinates D is described by 0 ≤ θ ≤ 2π, 0 ≤ r ≤ a. Let's compute I0 first: I0 = D (x2 + y2)rho dA = rho 2π 0 a 0 r2 r dr dθ = rho 2π 0 dθ a 0 r3 dr = 2πrho a 0 = . Instead of computing Ix and Iy directly, we use the facts that Ix + Iy = I0 and Ix = Iy (from the symmetry of the problem). Thus Ix = Iy = I0 2 = .

answer rather than having to add and subtract the measurements of the semi-circle, notice that the semicircle to the left of ad is actually identical in area to the blank semicircle-shaped space to the left of bc. so if we transferred the red semicircle into the blank space, we would end up with a square of side length 24 cm. the area of a square is s^2 = 24^2 = 676 cm^2.

u also answered this so i think u would know but i am here to

put in or use mine

51-50

step-by-step explanation:

triangle and cube

step-by-step explanation: