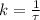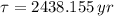Mathematics, 18.03.2020 02:24 katlynnschmolke
The amount A of the radioactive element radium in a sample decays at a rate proportional to the amount of radium present. Given the half-life of radium is 1690 years: (a) Write a differential equation that models the amount A of radium present at time t (b) Find the general solution of the differential equation. (c) Find the particular solution of the differential equation with the initial condition A(0)=10 g. (d) How much radium will be present in the sample at t=300 years?

Answers: 1


Other questions on the subject: Mathematics



Mathematics, 21.06.2019 19:50, Roshaan8039
Prove (a) cosh2(x) − sinh2(x) = 1 and (b) 1 − tanh 2(x) = sech 2(x). solution (a) cosh2(x) − sinh2(x) = ex + e−x 2 2 − 2 = e2x + 2 + e−2x 4 − = 4 = . (b) we start with the identity proved in part (a): cosh2(x) − sinh2(x) = 1. if we divide both sides by cosh2(x), we get 1 − sinh2(x) cosh2(x) = 1 or 1 − tanh 2(x) = .
Answers: 3
You know the right answer?
The amount A of the radioactive element radium in a sample decays at a rate proportional to the amou...
Questions in other subjects:


Chemistry, 10.11.2019 14:31






History, 10.11.2019 14:31

Biology, 10.11.2019 14:31

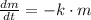 , b)
, b)  , c)
, c)  , d)
, d) 
 is the time constant and
is the time constant and