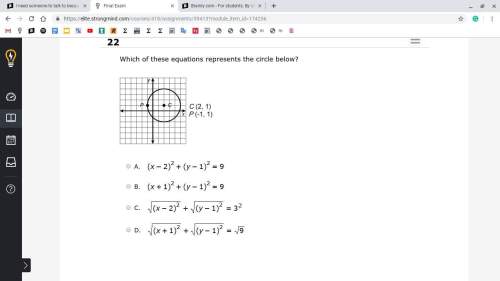
Mathematics, 13.12.2019 20:31 jamine
Solotion let p: rn+1∖{0}→rk+1∖{0} be a smooth function, and suppose that for some d∈z, p(λx)=λdp(x) for all λ∈r∖{0} and x∈rn+1∖{0}. (such a function is said to be homogeneous of degree d.) show that the map p~: rpn→rpk defined by p~([x])=[p(x)] is well defined and smooth.

Answers: 1


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 18:30, love123jones
Una caja de galletas contiene 16 paquetes y cada una de estas tiene 12 galletas y se quieren repartir entre 6 niños ¿de cuantas galletas le toca a cada niño?
Answers: 1

Mathematics, 21.06.2019 22:50, henryisasum7846
Jim had 15 minutes to do 5 laps around his school what would his time be
Answers: 1

Mathematics, 21.06.2019 23:50, jasminechambers642
What is the probably of getting heads when poing a coin and getting a number greater than or equal to 5 when rolling a single diea) 1/6b) 1/3c) 1/4d) 1/12
Answers: 2
You know the right answer?
Solotion let p: rn+1∖{0}→rk+1∖{0} be a smooth function, and suppose that for some d∈z, p(λx)=λdp(x)...
Questions in other subjects:





Physics, 16.11.2020 16:40


Mathematics, 16.11.2020 16:40