Mathematics, 24.10.2019 16:43 nickname0097
Part a. cooperative and competitive species in class, we have focused on first-order autonomous systems of differen- tial equations, such as the predator-prey systems described in section 2.1. in particular, we have seen how such systems can be studied using vector fields and phase plane analysis and how solution curves in the phase plane relate to the x(t)- and y(t)-graphs of the solutions. in this lab you will use these concepts and related numerical computations to study the behavior of the solutions to two different systems. we have discussed predator-prey systems at length. these are systems in which one species benefits while the other species is harmed by the interaction of the two species. in this lab you will study two other types of systems—competitive and cooperative systems. a competitive system is one in which both species are harmed by interaction, for example, cars and pedestrians. a cooperative system is one in which both species benefit from interaction, for example, bees and flowers. your overall goal is to understand what happens in both systems for all possible nonnegative initial conditions. several pairs of coopera- tive and competitive systems are given at the end of this lab. the analytic techniques that are appropriate to analyze these systems have not been discussed so far, so you will employ mostly geometric/qualitative and nu- meric techniques to establish your conclusions. since these are population models, you need consider only x and y in the first quadrant (x 0 and y > 0). systems: dx = -4x + 3xy = 5x – 2x2 - 4xy (i) (ii) laget -3y + 2xy = 7y - 4xy – 3y2 1. a brief discussion of all terms in each system. for example, what does the coefficient to the x term in equation for represent? which system is cooperative and which is competitive? 2. for each system, determine all relevant equilibrium points and ana- lyze the behavior of solutions whose initial conditions satisfy either xo = 0 or yo = 0. determine the curves in the phase plane along which the vector field is either horizontal or vertical. which way does the vector field point along these curves? 3. for each system, describe all possible population evolution scenarios using the phase portrait as well as x(t)- and y(t)-graphs. give spe- cial attention to the interpretation of the computer output (e. g. de tools) in terms of the long-term behavior of the populations

Answers: 1


Other questions on the subject: Mathematics

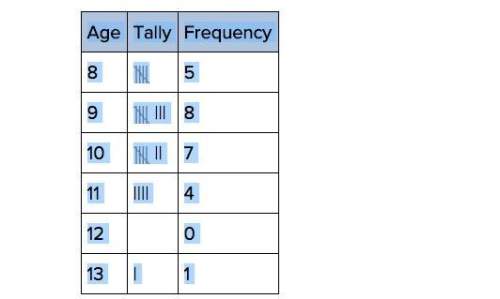
Mathematics, 21.06.2019 16:30, safiyabrowne7286
How do you summarize data in a two-way frequency table?
Answers: 3

Mathematics, 21.06.2019 19:30, KariSupreme
Which inequalities can be used to find the solution set of the following inequality? check all that apply. |2x – 5| (2x – 5) (2x + 5) –(2x – 5) –(2x + 5)
Answers: 1

Mathematics, 21.06.2019 22:40, Savannahh8503
Aclassmate thinks that solving a system by graphing gives an exact answer when the lines appear to cross at a grid point, but only an approximate answer when they don't. explain why this isn't true.
Answers: 3

Mathematics, 21.06.2019 22:40, winterblanco
Use this graph to find the cost of 6 show tickets
Answers: 1
You know the right answer?
Part a. cooperative and competitive species in class, we have focused on first-order autonomous syst...
Questions in other subjects:




Mathematics, 12.10.2020 19:01

Business, 12.10.2020 19:01


Mathematics, 12.10.2020 19:01

English, 12.10.2020 19:01

Mathematics, 12.10.2020 19:01