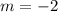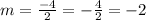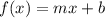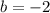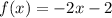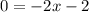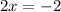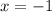Mathematics, 03.10.2019 02:30 jenniferalvarez360
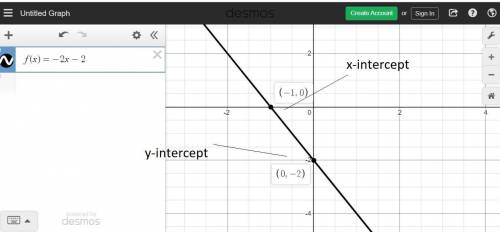
a linear function f models a relationship in which the dependent variable decreases 4 units for every 2 units the independent variable increases. the
value of the function at 0 is -2
identify the slope, y-intercept, and x-intercept of the graph

Answers: 3


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 23:40, hannahbannana98
Statement reason 1. δabc is similar to δced. given 2. 3. definition of slope 4. slope of slope of definition of slope 5. slope of × slope of multiplying the slopes 6. slope of × slope of substitution property of equality 7. slope of × slope of simplifying the right side the table contains the proof of the relationship between the slopes of two perpendicular lines. what is the reason for statement 2? a. parallel line segments that meet a common perpendicular line are proportional in length. b. the lengths of vertical and horizontal sides in congruent triangles are in a common ratio. c. trigonometric identities determine the lengths of the legs in a right triangle. d. corresponding side lengths in similar triangles are proportional in length.
Answers: 2

Mathematics, 22.06.2019 00:00, Lions8457
City l has a temperature of −3 °f. city m has a temperature of −7 °f. use the number line shown to answer the questions: number line from negative 8 to positive 8 in increments of 1 is shown. part a: write an inequality to compare the temperatures of the two cities. (3 points) part b: explain what the inequality means in relation to the positions of these numbers on the number line. (4 points) part c: use the number line to explain which city is warmer. (3 points)
Answers: 2

You know the right answer?
a linear function f models a relationship in which the dependent variable decreases 4 units for ever...
Questions in other subjects:


English, 19.07.2019 06:00


Mathematics, 19.07.2019 06:00





Biology, 19.07.2019 06:00