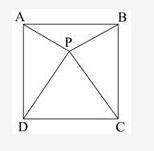
abcd is a square. p is a point inside the square. straight lines join points a and p, b and p, d and p, and c and p. triangle dpc is an equilateral triangle
jim makes the chart shown below to prove that triangle apd is congruent to triangle bpc:
statements justifications
in triangles apd and bpc; dp = pc sides of equilateral triangle dpc are equal
in triangles apd and bpc; ad = bc sides of square abcd are equal
in triangles apd and bpc; angle adp = angle bcp angle adc = angle bcd = 90° and
angle adp = angle bcp = 90° − 60° =
30°
triangles apd and bpc are congruent sss postulate
what is the error in jim's proof?
a. he writes dp = pc instead of dp = pb.
b. he writes ad = bc instead of ad = pc.
c. he assumes the measure of angle adp and angle bcp as 30° instead of 45°.
d. he assumes that the triangles are congruent by the sss postulate instead of sas postulate.

1/4 and 8/3 because:

the reciprocal if 4 is 1/4 because 4 is used as 4/1 and the opposite of that is 1/4. the opposite of 3/8 is 8/3 so that is the answer.

step-by-step explanation: given equation a = h(b 1+b 2)

also we are given values of a, h and b 1 as :

a = 16, h = 4, and b 1 = 3.

in order to solve it for b 2, we need to plug the given values of   a, h and b 1 .

therefore, plugging values of   a, h and b 1   in given equation, we get

16 = 4( 3 + b 2)

first dividing both sides by 4, we get

4 = 3 + b 2

subtracting 3 from both sides, we get

4 -3 = 3 -3 + b 2

1 = b 2.

2, 2, 2 or -4, 20, 29

step-by-step explanation:

there is two ways you can do it.

answer: the center is the median and/or mean of the data. the spread is the range of the data. and, the shape describes the type of graph. the four ways to describe shape are whether it is symmetric, how many peaks it has, if it is skewed to the left or right, and whether it is uniform. good luck

step-by-step explanation: