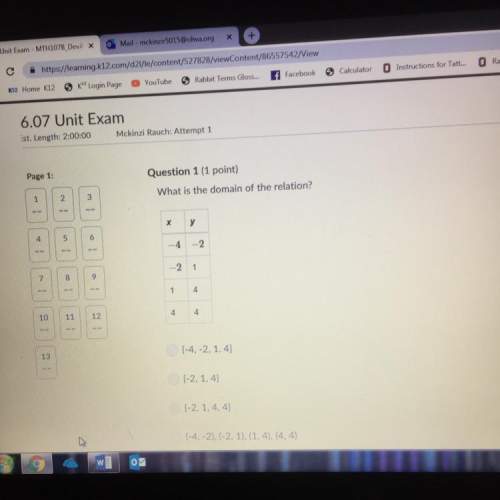
Mathematics, 28.08.2019 22:30 ManBun99
Let $abcd$ be a convex quadrilateral, and let $p$, $q$, $r$, $s$, $t$, $u$, $v$, and $w$ be the trisection points of the sides of $abcd$, as shown. [asy] unitsize(1 cm); pair a, b, c, d, p, q, r, s, t, u, v, w; a = (1,2); b = (4,3); c = (5,-1); d = (0,0); p = (2*a + b)/3; q = (a + 2*b)/3; r = (2*b + c)/3; s = (b + 2*c)/3; t = (2*c + d)/3; u = (c + 2*d)/3; v = (2*d + a)/3; w = (d + 2*a)/3; fill(a--q--r--c--u--v--cycle, gray(0.7)); draw(a--b--c--d--cycle); draw(q--r); draw(u--v); dot("$a$", a, nw); dot("$b$", b, ne); dot("$c$", c, se); dot("$d$", d, sw); dot("$p$", p, n); dot("$q$", q, n); dot("$r$", r, e); dot("$s$", s, e); dot("$t$", t, dir(270)); dot("$u$", u, dir(270)); dot("$v$", v, nw); dot("$w$", w, nw); [/asy] if the area of quadrilateral $abcd$ is 180, then find the area of hexagon $aqrcuv$.

Answers: 2


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 23:00, spaigenicole
Someone answer this asap for the first five terms of a sequence are shown. 5, 11, 23, 47, 95, . . which recursive function defines the nth term in the sequence for n > 1? a. f(n) = f(n - 1) + 6 b) f(n) = f(n - 1) + 48 c) f(n) = 3 • f(n - 1) + 1 d) f(n) = 3 • f(n - 1) - 4
Answers: 1

Mathematics, 22.06.2019 01:00, catycait27p5rc5p
5. write an equation for the line that is parallel to the given line and that passes through the given point. y = –5x + 3; (–6, 3)
Answers: 2

Mathematics, 22.06.2019 02:00, lala158736
Which of the following choices gives you a slope of 3?
Answers: 1

Mathematics, 22.06.2019 02:00, torquishag
Tanyss's house has 25 windows. her brother has washed 22 of the windows. what percent of the windows has her brother washed?
Answers: 1
You know the right answer?
Let $abcd$ be a convex quadrilateral, and let $p$, $q$, $r$, $s$, $t$, $u$, $v$, and $w$ be the tris...
Questions in other subjects:

Mathematics, 03.06.2020 20:57

Mathematics, 03.06.2020 20:57

Physics, 03.06.2020 20:57


English, 03.06.2020 20:57

History, 03.06.2020 20:57


Mathematics, 03.06.2020 20:57

Chemistry, 03.06.2020 20:57