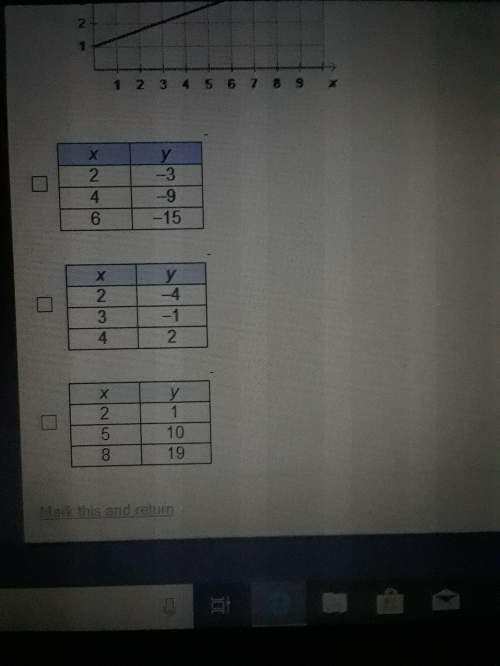
Mathematics, 30.06.2019 01:10 jacob7758
Let {an} be a bounded sequence of numbers in r. we define a new sequence bn} as follows sup{an n n} = 1. prove that {by} is monotone. definition. if {an} is a bounded sequence in r, then the limsup, denoted lim sup an, is defined as: n oo lim sup an n > n} lim sup an (1) noo n oo 2. prove that the limit in (1) exists. 3. based on the definition of the lim sup above, what would the definition of lim inf be? 4. using the definition you gave in the previous problem, show that for bounded sequences, the lim inf always exists 5. prove that if lm sup{an} lim inffan} l. then the limit of {an} exists and equals l

Answers: 2


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:40, natalie4085
Use properties to rewrite the given equation. which equations have the same solution as 2.3p – 10.1 = 6.5p – 4 – 0.01p?
Answers: 2

Mathematics, 21.06.2019 18:00, ethangeibel93
What set does not contain -3 the set of all real numbers the set of all integers the set of all whole numbers the set of all rational numbers
Answers: 1


Mathematics, 21.06.2019 20:00, lorip7799ov3qr0
The total number of dental clinics total for the last 12 months was recorded
Answers: 3
You know the right answer?
Let {an} be a bounded sequence of numbers in r. we define a new sequence bn} as follows sup{an n n}...
Questions in other subjects:

Biology, 12.12.2020 16:10

History, 12.12.2020 16:10

History, 12.12.2020 16:10

English, 12.12.2020 16:10

Mathematics, 12.12.2020 16:10


History, 12.12.2020 16:10

History, 12.12.2020 16:10

Mathematics, 12.12.2020 16:10

Mathematics, 12.12.2020 16:10