
Mathematics, 22.06.2019 21:10 luzcastellanos556
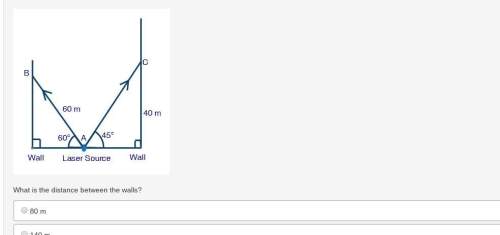
Asource of laser light sends rays ab and ac toward two opposite walls of a hall. the light rays strike the walls at points b and c, as shown below: a source of laser light is at point a on the ground between two parallel walls. the walls are perpendicular to the ground. ab is a ray of light which strikes the wall on the left at point b. the length of ab is 60m. ac is a ray of light which strikes the wall on the right at point c which is 40m above the ground. the ray ab makes an angle of 60 degrees with the ground. the ray ac makes an angle of 45 degrees with the ground. what is the distance between the walls? 80 m 140 m 70 m 110 m

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 16:30, victoria8281
Answer the following for 896.31 cm= km 100cm = 1m 1000m = 1km a) 0.0089631 b) 0.0089631 c) 8.9631 d) 89.631
Answers: 1


Mathematics, 21.06.2019 17:30, emiller6462
Use the net as an aid to compute the surface area of the triangular prism. a) 550 m2 b) 614 m2 c) 670 m2 d) 790 m2
Answers: 1

Mathematics, 21.06.2019 22:00, Ezonthekid
What is the value of the discriminant of the quadratic equation -2x = -8x + 8 and what does its value mean about thenumber of real number solutions the equation has?
Answers: 3
You know the right answer?
Asource of laser light sends rays ab and ac toward two opposite walls of a hall. the light rays stri...
Questions in other subjects:


Biology, 23.10.2019 20:50

Chemistry, 23.10.2019 20:50



Social Studies, 23.10.2019 20:50



English, 23.10.2019 20:50

History, 23.10.2019 20:50



