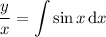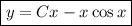Mathematics, 22.06.2019 21:00 luzcastellanos556
Find the general solution of the given differential equation. x dy dx − y = x2 sin(x) give the largest interval over which the general solution is defined. (think about the implications of any singular points. enter your answer using interval notation.

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 16:00, bryce12351
An equation of the line tangent to y=x^3+3x^2+2 at its point of inflection is
Answers: 3



Mathematics, 22.06.2019 02:00, nathanstern21
Which polynomial correctly combines the like terms and expresses the given polynomial in standard form? 8mn5 – 2m6 + 5m2n4 – m3n3 + n6 – 4m6 + 9m2n4 – mn5 – 4m3n3 n6 + 7mn5 + 14m2n4 – 5m3n3 – 6m6 –2m6 – 5m3n3 + 14m2n4 + 7mn5 + n6 14m2n4 + 7mn5 – 6m6 – 5m3n3 + n6 n6 – 6m6 + 7mn5 + 14m2n4 – 5m3n3 show work
Answers: 3
You know the right answer?
Find the general solution of the given differential equation. x dy dx − y = x2 sin(x) give the large...
Questions in other subjects:

Advanced Placement (AP), 01.12.2020 17:40

English, 01.12.2020 17:40


Chemistry, 01.12.2020 17:40

Mathematics, 01.12.2020 17:40

Mathematics, 01.12.2020 17:40


History, 01.12.2020 17:40

Mathematics, 01.12.2020 17:40

Mathematics, 01.12.2020 17:40

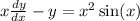 is
is 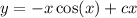 .The interval of the solution is
.The interval of the solution is 
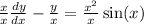
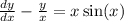
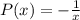
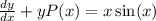
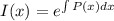
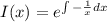
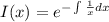
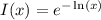
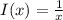
![[\frac{dy}{dx} -\frac{y}{x}] \frac 1x = [x \sin(x)] \frac 1x](/tpl/images/0005/4182/e89c3.png)
![[\frac{dy}{dx} -\frac{y}{x}] \frac 1x =\sin(x)](/tpl/images/0005/4182/3d2f0.png)
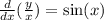
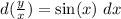
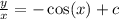
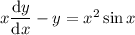
 . In doing so, we force any possible solutions to exist on either
. In doing so, we force any possible solutions to exist on either 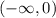 or
or 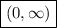 (the "positive" interval in such a situation is usually taken over the "negative" one) because
(the "positive" interval in such a situation is usually taken over the "negative" one) because  cannot be 0 in order for us to do this.
cannot be 0 in order for us to do this.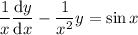
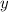 :
:![\dfrac{\mathrm d}{\mathrm dx}\left[\dfrac yx\right]=\sin x](/tpl/images/0005/4182/a69bc.png)