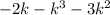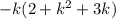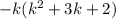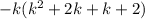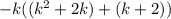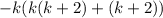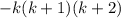Mathematics, 22.06.2019 21:00 hannahbannana98

Factor completely. -2k - k 3 - 3k 2 a.) k(-k + 1)(k - 2) b.) -k(k - 1)(k - 2) c.) -k(k + 1)(k + 2)

Answers: 1

Show answers

Other questions on the subject: Mathematics

Mathematics, 21.06.2019 18:00, ethangeibel93

What set does not contain -3 the set of all real numbers the set of all integers the set of all whole numbers the set of all rational numbers

Answers: 1

continue

Mathematics, 21.06.2019 19:00, GL1TCHED

What is the average diastolic blood pressure for adults

Answers: 2

continue

Mathematics, 21.06.2019 21:50, xojade

6x + 3y = -6 2x + y = -2 a. x = 0, y = -2 b. infinite solutions c. x = -1, y = 0 d. no solution

Answers: 1

continue

Mathematics, 21.06.2019 22:30, kingoc321

What is the distance between a and b? round your answer to the nearest tenth. a coordinate plane is shown. point a is located at negative 1, 5, and point b is located at 4, 1. a line segment connects the two points.

Answers: 1

continue

You know the right answer?

Factor completely. -2k - k 3 - 3k 2 a.) k(-k + 1)(k - 2) b.) -k(k - 1)(k - 2) c.) -k(k + 1)(k + 2)...

Questions in other subjects:

Mathematics, 10.09.2019 06:10

M= 175°, zcb m = 45x - 3, and dcz m = 15x - 2. find dcz...

Mathematics, 10.09.2019 06:10

41,373 rounded to the nearest thousand is...

History, 10.09.2019 06:10

O20q000 many immigrants to the united states in the late twentieth century came from europe and latin america. o europe and africa, o africa and asia....

Mathematics, 10.09.2019 06:10

Raj is mixing different colors of paint. the table shows the amount of each color paint raj uses for each mixture. select the two mixtures that will create the same color.

English, 10.09.2019 06:10

In the opening of the declaration of independence, thomas jefferson introduces what distinctly american political thought? kings have the right to rule despite their persona...

History, 10.09.2019 06:10

Describe the supreme court's general interpretation of the constitution under chief justice john marshall...

Spanish, 10.09.2019 06:10

How do two unknown females greet each other in a business meeting in spanish...

Mathematics, 10.09.2019 06:10

Ill give brainliest me georgette needs to earn a b in her physics class. her current test scores are 80, 83, 77, and 89. her final exam is worth 3 test scores. in order to...

English, 10.09.2019 06:10

Which sentence would not fit in a paragraph about composting? o a. you can also recycle your paper, glass, and plastics to the environment. o b. the...

Mathematics, 10.09.2019 06:10

Seven times five times six plus eight...

More questions: Mathematics Another questions