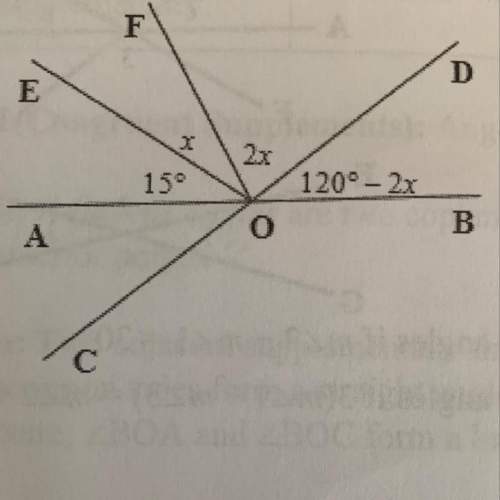
The following figures are not drawn to scale but ab and cd are straight lines. find x
...

Mathematics, 22.06.2019 21:20 ddarby
The following figures are not drawn to scale but ab and cd are straight lines. find x

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 17:30, liquidmana42
When the solutions to each of the two equations below are graphed in the xy-coordinate plane, the graphs of the solutions intersect at two places. write the y-cordninates of the points of intersection in the boxes below in order from smallest to largest. y=2x y=x^2-3
Answers: 1

Mathematics, 21.06.2019 19:30, ashtonsilvers2003
Evaluate the expression for the given value of the variable. ∣-4b-8∣+∣-1-b^2 ∣+2b^3 ; b=-2
Answers: 2

Mathematics, 21.06.2019 20:00, janeriaw188
Afamily has five members. a mom, a dad, two sisters, & a brother. the family lines up single file. what is the probabillity that the mom is at the front of the line
Answers: 1

Mathematics, 21.06.2019 21:20, KennyMckormic
The radius of the circle below intersects the unit circle at (3/5,4/5). what is the approximate value of theta? 0.6 radians 1.0 radians 36.9 degrees 53.1 degrees
Answers: 3
You know the right answer?
Questions in other subjects:




Mathematics, 29.04.2022 21:10






SAT, 29.04.2022 21:50



