
Mathematics, 12.11.2019 06:31 allieallie
At a manufacturing plant where switches are made, it is a known fact that 2% of all switches are defective. if two switches are used in a device, what is the probability that exactly one switch is good?

Answers: 3


Other questions on the subject: Mathematics


Mathematics, 21.06.2019 19:30, morganamandro9437
[15 points]find the quotient with the restrictions. (x^2 - 2x - 3) (x^2 + 4x + 3) ÷ (x^2 + 2x - 8) (x^2 + 6x + 8)
Answers: 1

Mathematics, 21.06.2019 23:00, kj44
Each of the following data sets has a mean of x = 10. (i) 8 9 10 11 12 (ii) 7 9 10 11 13 (iii) 7 8 10 12 13 (a) without doing any computations, order the data sets according to increasing value of standard deviations. (i), (iii), (ii) (ii), (i), (iii) (iii), (i), (ii) (iii), (ii), (i) (i), (ii), (iii) (ii), (iii), (i) (b) why do you expect the difference in standard deviations between data sets (i) and (ii) to be greater than the difference in standard deviations between data sets (ii) and (iii)? hint: consider how much the data in the respective sets differ from the mean. the data change between data sets (i) and (ii) increased the squared difference îł(x - x)2 by more than data sets (ii) and (iii). the data change between data sets (ii) and (iii) increased the squared difference îł(x - x)2 by more than data sets (i) and (ii). the data change between data sets (i) and (ii) decreased the squared difference îł(x - x)2 by more than data sets (ii) and (iii). none of the above
Answers: 2

Mathematics, 22.06.2019 01:30, justsuz72p71a21
Given the functions, f(x) = 2x^2 - 1 and g(x) = 5x, find f(g(x)) and g(f(
Answers: 2
You know the right answer?
At a manufacturing plant where switches are made, it is a known fact that 2% of all switches are def...
Questions in other subjects:

Mathematics, 05.12.2020 18:00


Social Studies, 05.12.2020 18:00



Geography, 05.12.2020 18:00

Mathematics, 05.12.2020 18:00



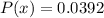
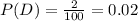
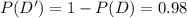
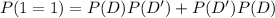
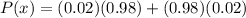
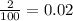
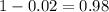
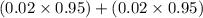 = 0.0392
= 0.0392

