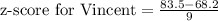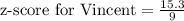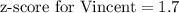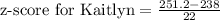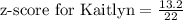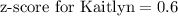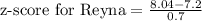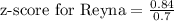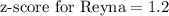Mathematics, 22.06.2019 21:00 fazegaze89
Three potential employees took an aptitude test. each person took a different version of the test. the scores are reported below. vincent got a score of 83.583.5; this version has a mean of 68.268.2 and a standard deviation of 99. kaitlyn got a score of 251.2251.2; this version has a mean of 238238 and a standard deviation of 2222. reyna got a score of 8.048.04; this version has a mean of 7.27.2 and a standard deviation of 0.70.7. if the company has only one position to fill and prefers to fill it with the applicant who performed best on the aptitude test, which of the applicants should be offered the job?

Answers: 3


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 21:30, camdenmorrison
At the county fair, the baxter family bought 6 hot dogs and 4 juice drinks for $12.90. the farley family bought 3 hot dogs and 4 juice drinks for $8.55. find the price of a hot dog and the price of a juice drink.
Answers: 1

Mathematics, 21.06.2019 23:10, ineedhelp2285
The input to the function is x and the output is y. write the function such that x can be a vector (use element-by-element operations). a) use the function to calculate y(-1.5) and y(5). b) use the function to make a plot of the function y(x) for -2 ≤ x ≤ 6.
Answers: 1

Mathematics, 22.06.2019 01:00, Kikilcaro4423
First work with stencil one. use a combination of reflections, rotations, and translations to see whether stencil one will overlap with the original pattern. list the sequence of rigid transformations you used in your attempt, noting the type of transformation, the direction, the coordinates, and the displacement
Answers: 3

Mathematics, 22.06.2019 02:00, FaygoMango
Prove the following(cot0+cosec0)[tex](cot0 + cosec0) { }^{2} = \frac{1 + cos0}{1 - cos0} [/tex]
Answers: 1
You know the right answer?
Three potential employees took an aptitude test. each person took a different version of the test. t...
Questions in other subjects:





Biology, 04.07.2021 03:50


Mathematics, 04.07.2021 03:50

Computers and Technology, 04.07.2021 03:50


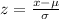 , where,
, where, = z-score,
= z-score, = Random sample score,
= Random sample score,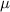 = Mean,
= Mean,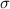 = Standard deviation.
= Standard deviation.