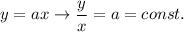Mathematics, 22.06.2019 21:00 evelin2318
Which equation represents a proportional relationship? a = y = -3x + 2 b = y = -2x +4 c = y = 4x d = y = x + 7

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 18:50, umarhaley
The avenues in a particular city run north to south and are numbered consecutively with 1st avenue at the western border of the city. the streets in the city run east to west and are numbered consecutively with 1st street at the southern border of the city. for a festival, the city is not allowing cars to park in a rectangular region bordered by 5th avenue to the west. 9th avenue to the east, 4th street to the south, and 6th street to the north. if x is the avenue number and yis the street number, which of the following systems describes the region in which cars are not allowed to park? 5th ave 9th ave
Answers: 1

Mathematics, 21.06.2019 21:30, Countryqueen525
How do your peer relationships affect your overall health status? what can you do to improve your peer relationships?
Answers: 1

Mathematics, 21.06.2019 22:30, gilcarrillo146
Micheal is 4 times as old as brandon and is also 27 years older than brandon. how old is micheal
Answers: 2
You know the right answer?
Which equation represents a proportional relationship? a = y = -3x + 2 b = y = -2x +4 c = y = 4x d...
Questions in other subjects:


Mathematics, 01.04.2020 01:31



Mathematics, 01.04.2020 01:31




Physics, 01.04.2020 01:31