Mathematics, 22.06.2019 21:00 karmaxnagisa20

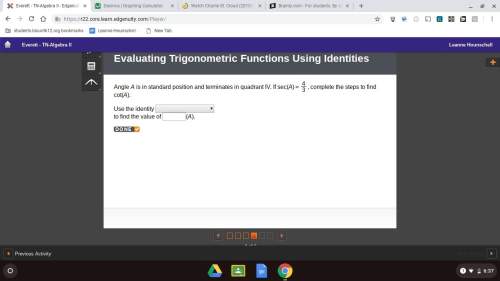
Options for the one with the drop down menu: sin^2(a)+cos^2(a)=1 tan^2(a)+1=sec^2(a) 1+cot^2(a)=csc^2(a)

Options for the one with the drop down menu: sin^2(a)+cos^2(a)=1 tan^2(a)+1=sec^2(a) 1+cot^2(a)=csc

Answers: 1

Show answers

Other questions on the subject: Mathematics

Mathematics, 21.06.2019 21:30, JeroMii

If f(x)=x+7 and g(x)=1/x what is (fog)(x)

Answers: 1

continue

Mathematics, 21.06.2019 23:00, moncho6222

72 the length of a side of a triangle is 36. a line parallel to that side divides the triangle into two parts of equal area. find the length of the segment determined by the points of intersection between the line and the other two sides of the triangle.

Answers: 1

continue

Mathematics, 22.06.2019 02:30, lisnel

Aconstruction worker needs to put a rectangular window in the side of a building he knows from measuring that the top and bottom of the window have a width of 8bfeet and the sides have a length of 15 feet he also measured one diagonal to be 17 feet what is the length of the other diagonal

Answers: 1

continue

Mathematics, 22.06.2019 02:30, avagymnast421

Kate is arranging new furniture in her rectangular sitting room. she has mapped the arrangement on a coordinate pane. a, b and c represent the sofas, v1 and v2 are decorative vases and aq the aquarium. find the distance between v1 and the aquarium. any body you

Answers: 3

continue

You know the right answer?

Options for the one with the drop down menu: sin^2(a)+cos^2(a)=1 tan^2(a)+1=sec^2(a) 1+cot^2(a)=csc...