Mathematics, 22.06.2019 21:00 Wemaybewrong
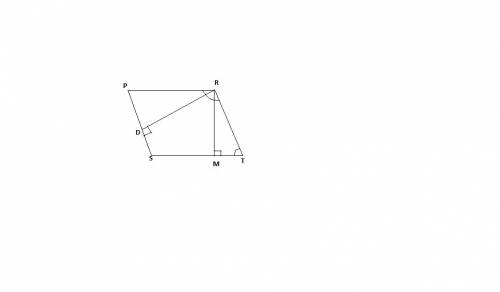
Given: prst is a parallelogram m∠t: m∠r=1: 3, rd ⊥ ps , rm ⊥ st find: m∠drm

Answers: 2


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 18:00, hendersontianna05
Pat listed all the numbers that have 15 as a multiple write the numbers in pats list
Answers: 3

Mathematics, 21.06.2019 18:40, miguel3maroghi
Some boys and girls were asked if they had a pet. one third of the group were boys. there were 20 boys. 20% of the girls had a pet. boys with a pet : girls with a pet = 1 : 5 i need to know how many girls there are.
Answers: 3


Mathematics, 21.06.2019 21:30, emilyplays474
Which of the following is a solution of z^6 = 64i? 2(cos105° + isin105°) 2(cos120° + isin120°) 2(cos135° + isin135°) 8(cos15° + isin15°)
Answers: 1
You know the right answer?
Given: prst is a parallelogram m∠t: m∠r=1: 3, rd ⊥ ps , rm ⊥ st find: m∠drm...
Questions in other subjects:

Mathematics, 18.03.2021 02:30


English, 18.03.2021 02:30



Social Studies, 18.03.2021 02:30

Mathematics, 18.03.2021 02:30


English, 18.03.2021 02:30

Mathematics, 18.03.2021 02:30