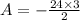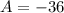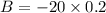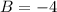Mathematics, 22.06.2019 21:00 yariiixox
Point's a and b are to be mapped onto a number line according to two equations. the solution to the equation 2/3a = -24 is the coordinate of point a. the solution to the equation 20 = -b/0.2 is the coordinate of point b.(a) solve the equation to find the coordinate of point a. show your work.(b) solve the second equation to find the coordinate of point b. show your work.(c) determine the distance between points a and b. explain. now! i really need this today!

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 20.06.2019 18:02, lacourboud20005
Ineed on 32 and 34! show work! correct gets brainliest! 50 points
Answers: 1

Mathematics, 20.06.2019 18:04, jake2920
Movie $5.50 soda $1.75 popcorn $2.25 candy bar $1.10 jeffrey left home with $20 in his wallet. he had a quick lunch that cost $8.47 and went to the movie theater. which of these activities can jeffrey do? a) go to movie and take two friends b) go to movie and have a soda, a popcorn and a candy bar c) go to movie, take a friend, and have a popcorn to share d) go to a movie, have 2 popcorns, 2 sodas, and 2 candy bars eliminate
Answers: 2


Mathematics, 21.06.2019 16:30, VgCarlos2596
What are “like terms”? why can we only add like terms?
Answers: 1
You know the right answer?
Point's a and b are to be mapped onto a number line according to two equations. the solution to the...
Questions in other subjects:




History, 19.05.2020 20:59


English, 19.05.2020 20:59


Mathematics, 19.05.2020 20:59


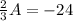 is the coordinate of point A.
is the coordinate of point A. 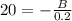 is the coordinate of point B.
is the coordinate of point B.