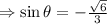Mathematics, 28.06.2019 13:00 bcox32314
Cos(−θ)=√3/3, sinθ< 0 what is the value of sin θ? 2√3/3 - √6/3 - 2√3/3 √6/3

Answers: 1


Other questions on the subject: Mathematics

Mathematics, 21.06.2019 14:30, bossninja97588
Multiply −2x(6x^4−7x^2+x−5) express the answer in standard form. enter your answer in the box.
Answers: 3

Mathematics, 21.06.2019 17:30, 21villalobosjabez
Trent wants to buy 2 packs of trading cards for 3 dollars each. the trading card packs that trent normally buys tend to come in packs of 6, 10, 12, or 15 cards. after selecting 2 packs, trent found that the first pack of cards cost 25 cents per card, and the second pack cost 30 cents per card. trent uses this information to write the equations below in order to compare c, the number of cards in each pack.
Answers: 2

Mathematics, 21.06.2019 19:00, fatherbamboo
What is the best way to answer questions with a x expression in the question. for example 3x + 10x=?
Answers: 1

Mathematics, 21.06.2019 19:30, mary9590
Cone w has a radius of 8 cm and a height of 5 cm. square pyramid x has the same base area and height as cone w. paul and manuel disagree on how the volumes of cone w and square pyramid x are related. examine their arguments. which statement explains whose argument is correct and why? paul manuel the volume of square pyramid x is equal to the volume of cone w. this can be proven by finding the base area and volume of cone w, along with the volume of square pyramid x. the base area of cone w is π(r2) = π(82) = 200.96 cm2. the volume of cone w is one third(area of base)(h) = one third third(200.96)(5) = 334.93 cm3. the volume of square pyramid x is one third(area of base)(h) = one third(200.96)(5) = 334.93 cm3. the volume of square pyramid x is three times the volume of cone w. this can be proven by finding the base area and volume of cone w, along with the volume of square pyramid x. the base area of cone w is π(r2) = π(82) = 200.96 cm2. the volume of cone w is one third(area of base)(h) = one third(200.96)(5) = 334.93 cm3. the volume of square pyramid x is (area of base)(h) = (200.96)(5) = 1,004.8 cm3. paul's argument is correct; manuel used the incorrect formula to find the volume of square pyramid x. paul's argument is correct; manuel used the incorrect base area to find the volume of square pyramid x. manuel's argument is correct; paul used the incorrect formula to find the volume of square pyramid x. manuel's argument is correct; paul used the incorrect base area to find the volume of square pyramid x.
Answers: 3
You know the right answer?
Cos(−θ)=√3/3, sinθ< 0 what is the value of sin θ? 2√3/3 - √6/3 - 2√3/3 √6/3...
Questions in other subjects:


English, 25.06.2019 11:00




Mathematics, 25.06.2019 11:00

Mathematics, 25.06.2019 11:00

Mathematics, 25.06.2019 11:00


Arts, 25.06.2019 11:00

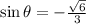
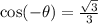 .
.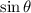 .
.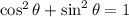
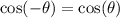
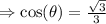 .
.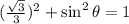
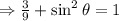
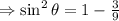
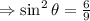
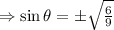
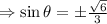
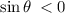 , so we choose the negative value.
, so we choose the negative value.