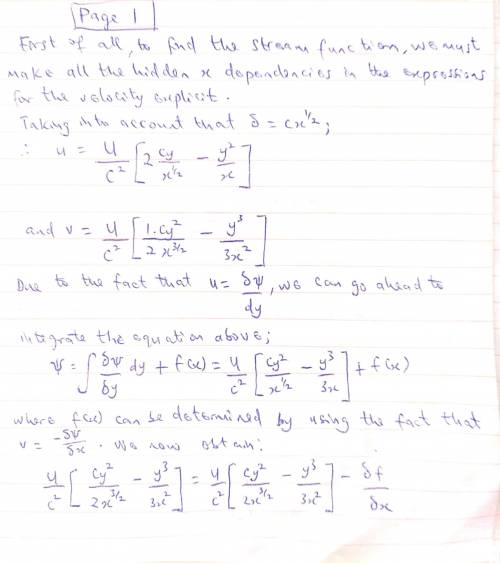Engineering, 27.02.2020 23:25 JellalFernandes

A useful approximation for the x component of velocity in an incompressible laminar boundary layer is a parabolic variation from u = 0 at the surface (y = 0) to the freestream velocity, U, at the edge of the boundary layer (y = δ). The equation for the profile is u/U = 2(y/δ) - (y/δ)2, where δ = cx1/2 and c is a constant. (a) Derive the stream function for this flow field. Locate streamlines at (b) "one-quarter" and (c) one-half the total volume flow rate in the boundary layer.

Answers: 2

Show answers

Other questions on the subject: Engineering

Engineering, 03.07.2019 23:20, abbz13

Two technicians are discussing the intake air temperature (iat) sensor. technician a says that the computer uses the iat sensor as a backup to the engine coolant temperature (ect) sensor. technician b says that the powertrain control module (pcm) will subtract the calculated amount of fuel if the air measures hot. who is correct

Answers: 3

continue

Engineering, 04.07.2019 18:10, ashleybaber4966

If a particle moves along a path such that r : (3 sin t) m and ? : 2t rad, where t is in seconds. what is the particle's acceleration in m/s in 4 seconds? a)- 16.43 b)- 16.29 c)- 15.21 d)- 13.79

Answers: 1

continue

Engineering, 04.07.2019 18:10, tjeffers90028

Refrigerant 134a enters an insulated compressor operating at steady state as saturated vapor at -26°c with a volumetric flow rate of 0.18 m3/s. refrigerant exits at 9 bar, 70°c. changes in kinetic and potential energy from inlet to exit can be ignored. determine the volumetric flow rate at the exit, in m3/s, and the compressor power, in kw.

Answers: 1

continue

Engineering, 04.07.2019 19:10, Mimidj9279

The sum of the normal stresses does not change as the stress state rotates through an angle. a)-trune b)- false

Answers: 2

continue

You know the right answer?

A useful approximation for the x component of velocity in an incompressible laminar boundary layer i...