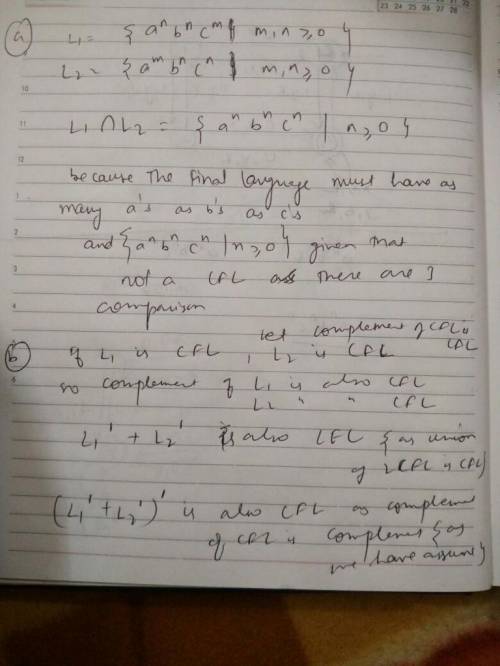Computers and Technology, 04.03.2020 01:34 McSporter

We have seen in class that the sets of both regular and context-free languages are closed under the union, concatenation, and star operations. We have also seen in A2 that the regular languages are closed under intersection and complement. In this question, you will investigate whether the latter also holds for context-free languages.
(a) Use the languages A = {a^mb^nc^n \ m, n greaterthanorequalto 0} and B = {a^nb^nc^m \ m, n greaterthanorequalto 0} to show that the class of context-free languages is not closed under intersection. You may use the fact that the language C = {a^nb^nc^n | n greaterthanorequalto 0} is not context-free.
(b) Using part (a) above, show now that the set of context-free languages is not closed under complement.

Answers: 1

Show answers

Other questions on the subject: Computers and Technology

Computers and Technology, 24.06.2019 07:00, jordaaan101

Guys do you know sh27 cause he hacked me : ( pidgegunderson my old user

Answers: 2

continue

Computers and Technology, 24.06.2019 07:30, LuckyCharms988

Consider the folloeing website url: what does the "http: //" represent? a. protocal identifier. b. ftp. c. domain name d. resource name

Answers: 2

continue

Computers and Technology, 24.06.2019 17:00, rosepetals2938

Carlos, an algebra teacher, is creating a series of powerpoint presentations to use during class lectures. after writing, formatting, and stylizing the first presentation, he would like to begin writing the next presentation. he plans to insert all-new content, but he wants to have the same formatting and style as in the first one. what would be the most efficient way for carlos to begin creating the new presentation? going under the file tab and opening the first presentation, deleting all content from each page, and adding new content going under the file tab and clicking on new in the left pane, then choosing new from existing going under the design tab and clicking on themes, then selecting the theme that was used for the first template going under the design tab and opening the template that was created for the first presentation

Answers: 2

continue

Computers and Technology, 24.06.2019 19:50, joThompson

Which is a characteristic of free and open-source software licenses? a. the source code is unavailable to everyone b. the source code is available only to the government c. the source code is available to all users d. the source code is constantly modified

Answers: 1

continue

You know the right answer?

We have seen in class that the sets of both regular and context-free languages are closed under the...